金属玻璃是合金熔体在急速冷却条件下形成的一种新型亚稳态材料。它有带状、丝状和块体等形式,具有广阔的应用前景。
金属玻璃内部原子接近长程无序、短程有序,不存在位错、晶界等缺陷决定了金属玻璃有高强度、高硬度、高弹性极限等优良性能,但在室温下它呈现非均匀变形,塑性变形也局限于极窄的剪切带内,限制了它实际应用的范围。
作者利用自由体积模型编写材料子程序,同时建立代表性体积单元(RVE)模型,最后分析了颗粒对MGCs的影响机制和颗粒体积分数、颗粒应变硬化指数、颗粒的间距、网状结构对MGCs拉伸塑性的影响。
1、计算模型
1.1金属玻璃基体本构方程
金属玻璃的基本变形机制是剪切带的形成和演化。剪切带形成与局部结构次序的演化有关,它是应变软化导致局部化变形的结果。为使本构关系具有捕捉剪切带的能力,自由体积模型引入自由体积作为状态变量。该模型假设在纯剪切情况下宏观塑性流动是净原子在外加应力方向上以跃迁的形式出现。
金属玻璃塑性流动方程如下:
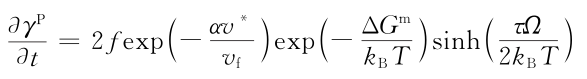
在外加应力情况下,应力驱动产生自由体积和结构弛豫湮灭自由体积相互竞争使结构重排。纯自由体积增加如下:
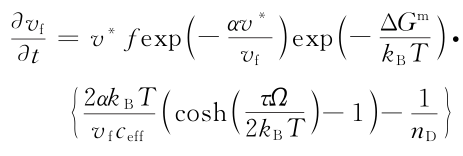
在多轴应力状态下,自由体积演变方程为:
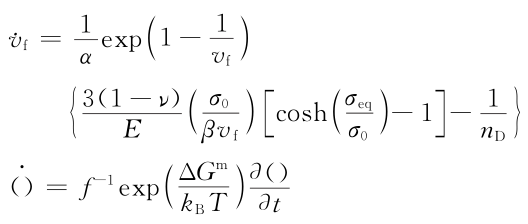
在上述自由体积模型中,剪切带演变被看成是内部状态变量,也就是在方程式中给出的标准自由体积Vf。自由体积场的演变很大程度上依赖于原来的应力状态和当时的自由体积场。
1.2颗粒的本构方程
颗粒满足J2塑性流动理论如下:
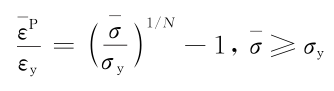
2、有限元计算模型
为了用有限元计算展现复合材料的微观机制,建立一个代表性体积单元(RVE)模型来描述复合材料的宏观力学性能。
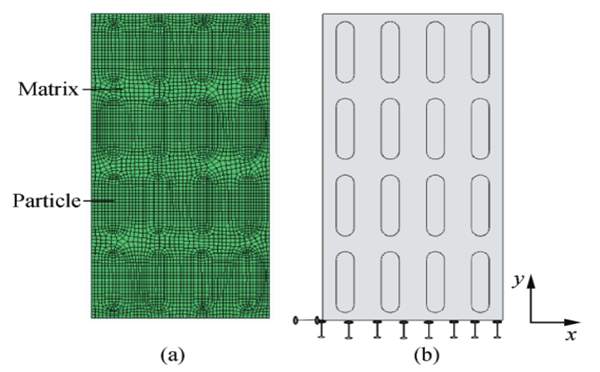
图1:颗粒体积分数为30%的MGCs的RVE模型
从本质上看,MGCs中包含着软硬不均匀区域,这些结构的不均匀性将会导致剪切转变区汇集和随后剪切带的形成与扩展。
3、结果讨论
3.1不同颗粒体积分数对MGCs的影响
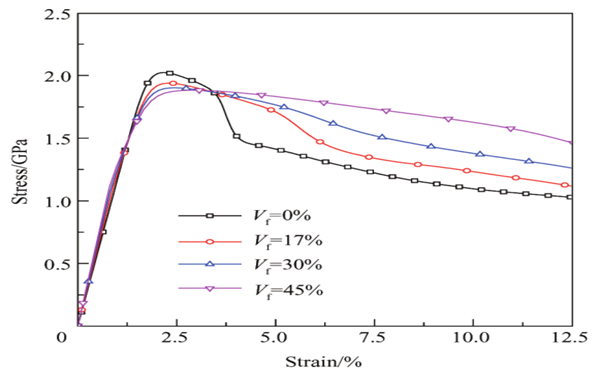
图2:颗粒体积分数不同的MGCs的应力-应变曲线
从图2可以看出,随着体积分数的增加,复合材料的塑性提高但牺牲了部分强度。
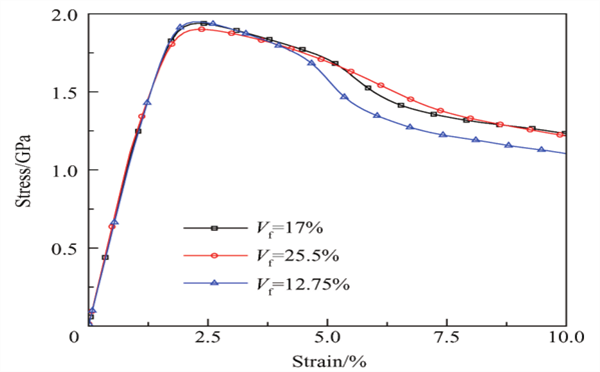
图3:颗粒大小相同、颗粒体积含量不同的MGCs的应力-应变曲线
从图3可以看出,随着颗粒体积分数的增加,复合材料的塑性增加。
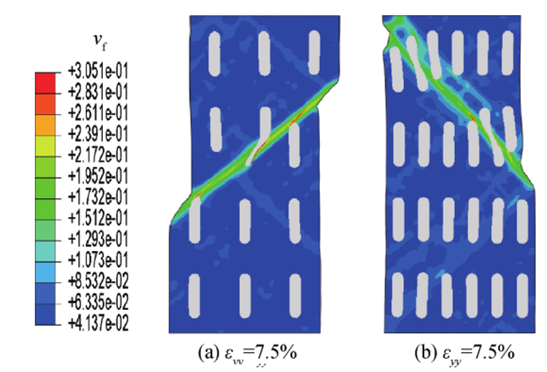
图4:MGCs中颗粒体积分数为12.75% (a)和25.5% (b)时的剪切带云图
从图4(b)中可以看出,体积分数为25.5%时,主剪切带在穿过颗粒的同时,也出现绕着颗粒扩展,使基体的应力下降缓慢,塑性增强,同时与体积分数为12.75%时相比,开始出现部分层状次级剪切带和剪切带交割,因此吸收更多变形能,韧性提高。
3.2 不同颗粒间距对MGCs的影响
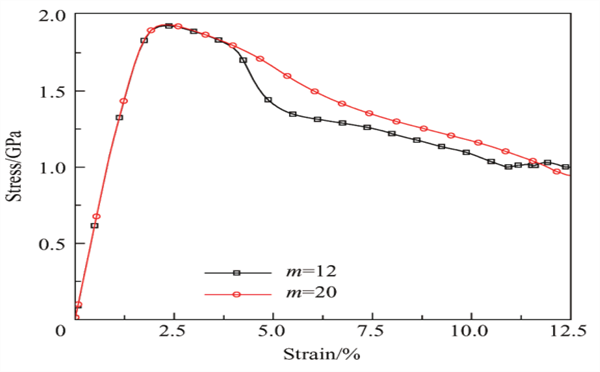
图5:MGCs 中不同颗粒间距时的应力-应变关系
通过改变颗粒的大小获得不同的间距。从图中可以看出,随着颗粒间距的减小即颗粒数的增加,复合材料的强度变化不明显,但塑性却有明显的增加。
3.3 不同硬化指数对MGCs的影响
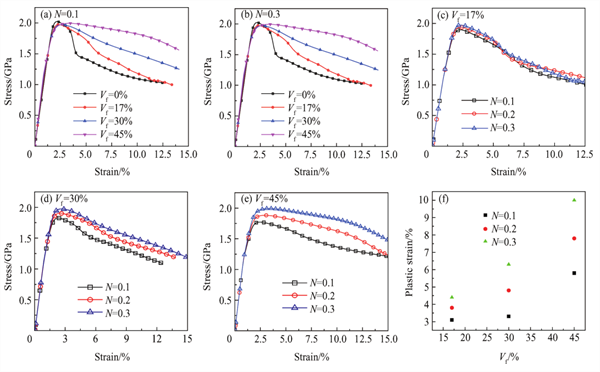
图6:MGCs中颗粒不同硬化指数时的应力-应变关系
对比硬化指数N =0.1的应力-应变曲线(如图6(a)所示)和硬化指数N=0.3的应力应变曲线(如图6(b)所示),都有5个阶段出现,而且颗粒体积分数提高最大时,应力强度降低,塑性应变增强。
但是硬化指数从N=0.1到N=0.3过程中,通过图6(c)~6(e)可知,都有一个相同的规律,即硬化指数高时塑性应变提高,而且最大应力强度提高。
3.4不同微结构对MGCs的影响
由颗粒的间距变化,联想到高体积分数颗粒会排布成类似丝瓜状的网状结构或者直接在复合材料中加入这种网状结构,增韧效果可能更好。
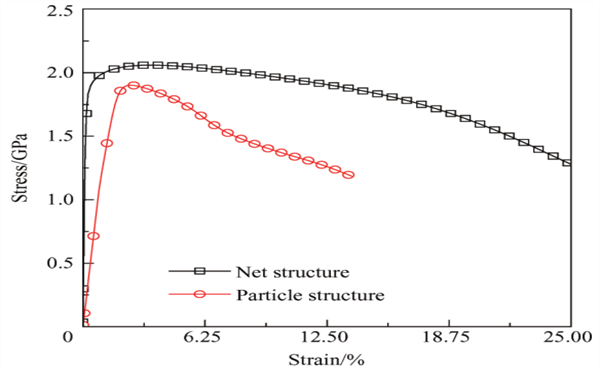
图7:MGCs中颗粒不同结构排列下MGCs的应力-应变关系
可以看出,网状结构的排列与颗粒竖直排列的结构相比,复合材料的强度不仅得到提高,弹性模量也增加,塑性也得到很大的增强。从图7(a)~(c)的变化过程中可以看出,网状结构随着荷载的增大,几乎是均匀变形,直到最后自由体积含量达到饱和,结构遭到破坏。因此弹性比提高,吸收变形能力提高,韧性增强。
4、结论
(1)随着颗粒体积分数的提高,金属玻璃复合材料( MGCs )的塑性增强,但牺牲了部分强度,尤其当体积分数达到45%时,材料的塑性得到很大的提高。
(2)随着颗粒间距的减小,MGCs的强度变化不大,但塑性得到了增强。
(3)随着颗粒硬化指数从0.1增大到0.3,MGCs的塑性和强度都得到提高。主要原因在于高强度颗粒更加有效地阻碍剪切带的快速扩展。
(4)颗粒结构如果能用同种材料的网状结构进行替代,可以发现,网状结构更能引起复合材料的均匀变形,进而增大复合材料的强度和韧性。







